Kernel 10: Incomplete tiles and arbitrary matrix sizes

2D register tiling has given us the biggest performance boost (and an increased amount of work per thread before that). So, maybe we can take this one step further, using the extra registers that are now available to us with 256 active threads. The obvious thing to do is increase the register blocking factors WPTN and WPTM from 8 by 8 to 16 by 16. However, that would already consume 256 registers for the accumulation values alone. So, a rectangular or a non-power-of-2 solution would be a more realistic solution.

Before we do anything else, we'll change our load code a bit, allowing us to change TSM and TSN independent of each other. This can cost a bit of performance, but it gives us some generality:

// Load one tile of A into local memory
for (int la=0; la<LPTA/WIDTH; la++) {
   int tid = tidn*RTSM + tidm;
   int id = la*RTSN*RTSM + tid;
   int row = id % (TSM/WIDTH);
   int col = id / (TSM/WIDTH);
   (...)
}
// Load one tile of B into local memory
for (int lb=0; lb<LPTB/WIDTH; lb++) {
   int tid = tidn*RTSM + tidm;
   int id = lb*RTSN*RTSM + tid;
   int row = id % (TSN/WIDTH);
   int col = id / (TSN/WIDTH);
   (...)
}

Now, if we want to apply 10 by 10 register blocking (or local memory tiling for that matter) to a 4096 by 4096 matrix for example, we'll end up with partially filled tiles. Since we don't have a 1-to-1 correspondence of thread IDs to data loads, we cannot simply add a big if-statement around the kernel to guard partial-tiles. What we can do is pad the input matrices with zeroes to create complete tiles and remove them from the output matrix afterwards.

Padding is done as shown below. We first extend the dimensions K, M, and N into multiples of the tile-sizes TSK, TSM, and TSN to obtain K', M', and N' respectively. Once we have the new arrays, we can proceed as for the earlier kernels, but now we multiply by zero in some cases.



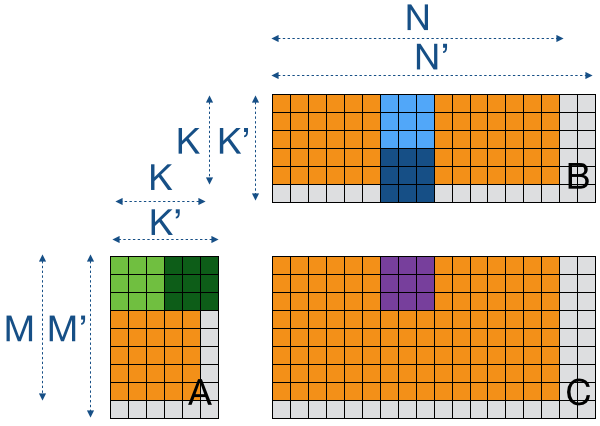
We use simple kernels to add padding to the input matrices A and B, and a similar kernel to remove padding from the output matrix C. The kernel to add padding is shown below:

// Pad the P * Q matrix with zeroes to form a P_XL * Q_XL matrix
__kernel void paddingAddZeroes(const int P, const int Q,
                               const __global float* input,
                               const int P_XL, const int Q_XL,
                               __global float* output) {
    
    // Thread identifiers
    const int tx = get_group_id(0)*PADDINGX + get_local_id(0); // 0..P_XL
    const int ty = get_group_id(1)*PADDINGY + get_local_id(1); // 0..Q_XL

    // Check whether we are within bounds of the XL matrix
    if (tx < P_XL && ty < Q_XL) {

        // Copy the input or pad a zero
        float value;
        if (tx < P && ty < Q) {
            value = input[ty*P + tx];
        }
        else {
            value = 0.0f;
        }

        // Store the result
        output[ty*P_XL + tx] = value;
    }
}

Note that we now run a total of 5 kernels: 2 to pad the input matrices, one to transpose the B matrix, one to perform the matrix-multiplication, and finally one to remove the padding from the output matrix. The 4 supporting kernels cost around 3% of the total execution time: not very significant, but it might be beneficial to combine transposing and padding or integrate these kernels into the remainder of your application.

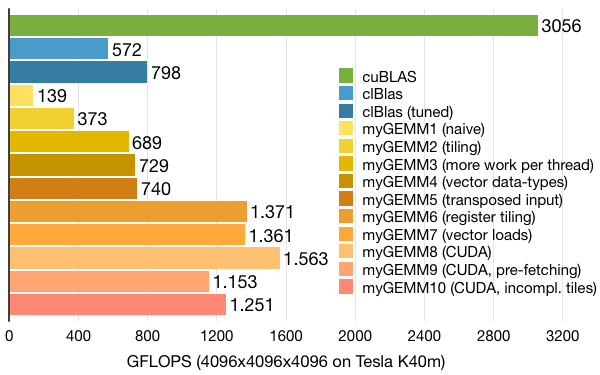
Running with tiles of 160 by 16 (matrix A), 16 by 160 (matrix B), and 160 by 160 (matrix C) enables 10 by 10 register blocking while running 16 by 16 threads with 64-bit vector loads. With this configuration, we make use of some of the additional available registers, increasing performance a bit over the previous version: from 1153 to 1251 GFLOPS. Unfortunately, this is not as good as our best version yet (running 512 instead of 256 active threads). On the positive side, the padding adds support for arbitrary matrix sizes, something that could very well be a requirement for real-life applications.

cnugteren.github.io