Kernel 3: More work per thread

One of the ways in which the previous kernel can be improved is by increasing the amount of work of each thread (and thus reducing the total number of threads). Why is this useful? Well, let's take a moment and inspect the PTX assembly that was generated for the previous kernel. In particular, let's look at the main computational part: the (unrolled) inner k-loop. Below are 2 of the TS iterations:

ld.shared.f32   %f50, [%r18+56];
ld.shared.f32   %f51, [%r17+1792];
fma.rn.f32  %f52, %f51, %f50, %f49;
ld.shared.f32   %f53, [%r18+60];
ld.shared.f32   %f54, [%r17+1920];
fma.rn.f32  %f55, %f54, %f53, %f52;

In each iteration of the k-loop, we see these three instructions:

1. The loading of an Asub element from the local memory into the register file (ld.shared.f32).
2. The loading of a Bsub element from the local memory into the register file (ld.shared.f32).
3. The actual computation in the form of a fused multiply add (fma.rn.f32).

Or, in simpler terms, only one of out three instructions are actual (useful) computations! Quite a waste of our precious GFLOPS, don't you think?

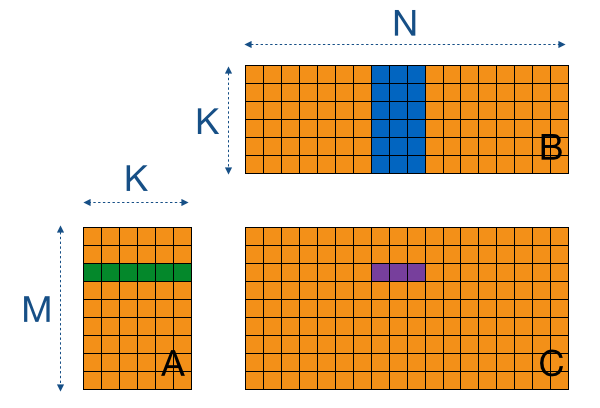
We can apply the same trick we did before with the tiling, but now at register-level. If we let one thread compute 8 elements arranged in consecutive columns of C, we can reduce accesses to A by a factor 8 (let's name this constant "WPT"). In this case, this reduction is not in terms of off-chip memory accesses (given that we keep our tiles at constant size), but in a reduced amount of local memory accesses. This is illustrated by the image below in which we (for simplicity) don't consider the tiling and use a WPT factor of 3.



Let's take a look at the new kernel, which brings the following changes:

• A factor of WPT registers are initialised to zero for each thread (lines 17 - 21).
• Each thread now loads WPT values of A and B into the local memory (lines 27 - 33). The tile-size is still the same, as is the amount of local memory used per work-group.
• Each thread performs WPT times TS accumulations per tile (lines 38 - 43). Note that the inner-most loop over WPT doesn't require a new value from Asub each time, saving precious local memory loads.
• Each thread stores WPT values in the resulting C matrix (lines 49 - 52).

// Increased the amount of work-per-thread by a factor WPT
__kernel void myGEMM3(const int M, const int N, const int K,
                      const __global float* A,
                      const __global float* B,
                      __global float* C) {
    
    // Thread identifiers
    const int row = get_local_id(0); // Local row ID (max: TS)
    const int col = get_local_id(1); // Local col ID (max: TS/WPT == RTS)
    const int globalRow = TS*get_group_id(0) + row; // Row ID of C (0..M)
    const int globalCol = TS*get_group_id(1) + col; // Col ID of C (0..N)

    // Local memory to fit a tile of TS*TS elements of A and B
    __local float Asub[TS][TS];
    __local float Bsub[TS][TS];

    // Initialise the accumulation registers
    float acc[WPT];
    for (int w=0; w<WPT; w++) {
        acc[w] = 0.0f;
    }
    
    // Loop over all tiles
    const int numTiles = K/TS;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        for (int w=0; w<WPT; w++) {
            const int tiledRow = TS*t + row;
            const int tiledCol = TS*t + col;
            Asub[col + w*RTS][row] = A[(tiledCol + w*RTS)*M + globalRow];
            Bsub[col + w*RTS][row] = B[(globalCol + w*RTS)*K + tiledRow];
        }
        
        // Synchronise to make sure the tile is loaded
        barrier(CLK_LOCAL_MEM_FENCE);

        // Perform the computation for a single tile
        for (int k=0; k<TS; k++) {
            for (int w=0; w<WPT; w++) {
                acc[w] += Asub[k][row] * Bsub[col + w*RTS][k];
            }
        }

        // Synchronise before loading the next tile
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // Store the final results in C
    for (int w=0; w<WPT; w++) {
        C[(globalCol + w*RTS)*M + globalRow] = acc[w];
    }
}

Since we increased the amount of work per thread, let's not forget to reduce the total amount of threads before we launch our kernel:

const size_t local[2] = { TS, TS/WPT };
const size_t global[2] = { M, N/WPT };

When we look at the new PTX assembly, we can see that we have greatly increased the fraction of FMA-instructions. For example, below are 8 iterations of the computation-loop (instead of the 2 from before), which show that we require only 8+1 loads from the local memory for 8 FMAs (instead of 8+8):

ld.shared.f32   %f82, [%r101+4];
ld.shared.f32   %f83, [%r102];
fma.rn.f32  %f91, %f83, %f82, %f67;
ld.shared.f32   %f84, [%r101+516];
fma.rn.f32  %f92, %f83, %f84, %f69;
ld.shared.f32   %f85, [%r101+1028];
fma.rn.f32  %f93, %f83, %f85, %f71;
ld.shared.f32   %f86, [%r101+1540];
fma.rn.f32  %f94, %f83, %f86, %f73;
ld.shared.f32   %f87, [%r101+2052];
fma.rn.f32  %f95, %f83, %f87, %f75;
ld.shared.f32   %f88, [%r101+2564];
fma.rn.f32  %f96, %f83, %f88, %f77;
ld.shared.f32   %f89, [%r101+3076];
fma.rn.f32  %f97, %f83, %f89, %f79;
ld.shared.f32   %f90, [%r101+3588];
fma.rn.f32  %f98, %f83, %f90, %f81;

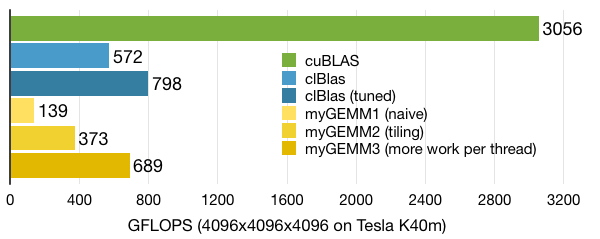
When we look at performance of our new kernel, it turns out we are already ahead of clBlas! Still, there are a couple of other tricks we can do to get more performance, as evidenced by the gap with cuBLAS.

cnugteren.github.io