Kernel 6: 2D register blocking

In one of our earlier kernels we increased the work per thread by a factor of 8. The motivation was that this would require less accesses to local memory, yielding a higher percentage of FMA instructions in the main computational loop. Let's take this idea one step further: we'll increase the work per thread in both dimensions to form so-called 2D 'register blocking'. This trick is very similar to what we've done for 2D tiling, but at a different memory level (from local memory to registers rather than from off-chip to local memory).

To get this working, we'll have to make a few changes. Let's start off with some fresh defines:

#define TSM 128                // The tile-size in dimension M
#define TSN 128                // The tile-size in dimension N
#define TSK 16                 // The tile-size in dimension K
#define WPTM 8                 // The work-per-thread in dimension M
#define WPTN 8                 // The work-per-thread in dimension N
#define RTSM (TSM/WPTM)        // The reduced tile-size in dimension M
#define RTSN (TSN/WPTN)        // The reduced tile-size in dimension N
#define LPTA ((TSK*TSM)/(RTSM*RTSN)) // Loads-per-thread for A
#define LPTB ((TSK*TSN)/(RTSM*RTSN)) // Loads-per-thread for B

We now have two work-per-thread variables, WPTM and WPTN. Both are set to 8, giving us work-groups of 16 by 16 (RTSM by RTSN) for tile-sizes in the M and N dimension of 128. We still consider TSM and TSN to be equal, making loading data a bit more concise since LPTA is equal to LPTB in that case.

We'll use the new WPTM and WPTN constants to compute the launch-parameters:

const size_t local[2] = { TSM/WPTM, TSN/WPTN }; // Or { RTSM, RTSN };
const size_t global[2] = { M/WPTM, N/WPTN };

The new kernel takes its basis from the previous kernel (myGEMM5). The following changes are made:

• The accumulation registers are now 2D: they are initialised using a double-loop. The results are also stored to the C matrix using a similar double-loop.
• Loading data has become even more complicated (but its worth it). We now put all the threads (in first and second dimension) onto one big pile, and add a loop over the amount of loads per threads (LPTA = LPTB) on top of that. This gives us the variable 'id', which we split by modulo and integer division to obtain the row and column IDs.
• In previous versions of the kernel we could cache a single value of Asub into a register and re-use it in the loop of WPT. Now, we make this explicit (using Areg) and do a similar trick for Bsub. However, for Breg we do need WPTN temporary registers, as its re-use is not in the inner-most loop.

// Use 2D register blocking (further increase in work per thread)
__kernel void myGEMM6(const int M, const int N, const int K,
                      const __global float* A,
                      const __global float* B,
                      __global float* C) {
    
    // Thread identifiers
    const int tidm = get_local_id(0); // Local row ID (max: TSM/WPTM)
    const int tidn = get_local_id(1); // Local col ID (max: TSN/WPTN)
    const int offsetM = TSM*get_group_id(0); // Work-group offset
    const int offsetN = TSN*get_group_id(1); // Work-group offset

    // Local memory to fit a tile of A and B
    __local float Asub[TSK][TSM];
    __local float Bsub[TSN][TSK+2];

    // Allocate register space
    float Areg;
    float Breg[WPTN];
    float acc[WPTM][WPTN];

    // Initialise the accumulation registers
    for (int wm=0; wm<WPTM; wm++) {
        for (int wn=0; wn<WPTN; wn++) {
            acc[wm][wn] = 0.0f;
        }
    }
    
    // Loop over all tiles
    int numTiles = K/TSK;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        for (int la=0; la<LPTA; la++) {
            int tid = tidn*RTSM + tidm;
            int id = la*RTSN*RTSM + tid;
            int row = id % TSM;
            int col = id / TSM;
            int tiledIndex = TSK*t + col;
            Asub[col][row] = A[tiledIndex*M + offsetM + row];
            Bsub[row][col] = B[tiledIndex*N + offsetN + row];
        }
        
        // Synchronise to make sure the tile is loaded
        barrier(CLK_LOCAL_MEM_FENCE);

        // Loop over the values of a single tile
        for (int k=0; k<TSK; k++) {

            // Cache the values of Bsub in registers
            for (int wn=0; wn<WPTN; wn++) {
                int col = tidn + wn*RTSN;
                Breg[wn] = Bsub[col][k];
            }

            // Perform the computation
            for (int wm=0; wm<WPTM; wm++) {
                int row = tidm + wm*RTSM;
                Areg = Asub[k][row];
                for (int wn=0; wn<WPTN; wn++) {
                    acc[wm][wn] += Areg * Breg[wn];
                }
            }
        }

        // Synchronise before loading the next tile
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // Store the final results in C
    for (int wm=0; wm<WPTM; wm++) {
        int globalRow = offsetM + tidm + wm*RTSM;
        for (int wn=0; wn<WPTN; wn++) {
            int globalCol = offsetN + tidn + wn*RTSN;
            C[globalCol*M + globalRow] = acc[wm][wn];
        }
    }
}

This new kernel is quite resource consuming and its performance can fluctuate quite a bit. Let's take a look at local memory usage first:
With the current settings (TSK = 16, TSM = TSN = 128), we use 16KB plus 1KB padding. With a total of 48KB local memory available, our best-case scenario is to get two work-groups running on a single SM at a time. With a work-group size of 256 (16 by 16) we'll have a total of 512 active threads to hide latencies.

But do we actually get to run 512 threads? The Kepler GPU has 64K 32-bit registers per SM, which gives us 128 registers per thread if we divide them over 512 threads. With our register-tiling technique, we use 8 by 8 accumulation registers, another 8 for B, and 1 for A. This gives us a lower limit of 73 registers, well below 128. Unfortunately, the compiler will use a lot more registers, making this 128 limit a real constraint. Some of these extra registers are used because of 'optimisations' to reduce the amount of instructions. For example, let's take a look at the following snippet from our kernel:

    // Loop over all tiles
    int numTiles = K/TSK;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        for (int la=0; la<LPTA; la++) {
            int tid = tidn*RTSM + tidm;
            int id = la*RTSN*RTSM + tid;
            int row = id % TSM;
            int col = id / TSM;
            (...)

The compiler will rightly conclude that each tile (iterations of the t-loop) requires the same index computations for 'row' and 'col' (based on 'id' and 'tid'). Therefore, to reduce the amount of instructions executed, the compiler will compute all LPTA values of row and col once before the tile-loop starts. Although this does save instructions, it also consumes 2*LPTA registers! Luckily we can tell the compiler to re-compute the values every time with the volatile-keyword:

volatile int id = la*RTSN*RTSM + tid;

For our kernel, running 256 or 512 active threads makes quite a difference. This makes our code very fragile and sensitive to compiler or small code changes (such as the volatile keyword above). Even compiler-options such as -cl-nv-maxrregcount=127 do not always help, as the compiler might decide to spill the extra registers it 'needs' to memory.

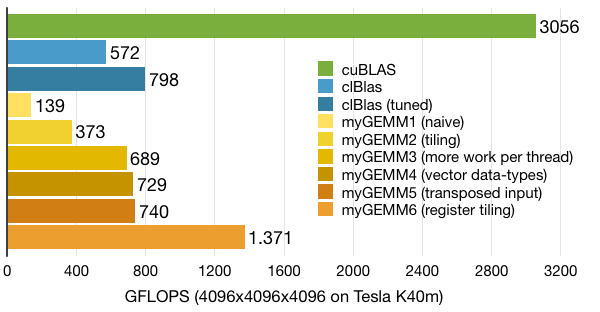
The best-case performance that we get from this kernel is well over 1.3 TFLOPS, more than twice the clBlas score! However, changing small things in the code (like using the volatile keyword or unrolling a particular loop) can bring us anywhere between 800 and 1300 GFLOPS. All in all, a significant improvement over previous kernels.

cnugteren.github.io