Tutorial: OpenCL SGEMM tuning for Kepler
Note: the complete source-code is available at GitHub.Note2: a tuned OpenCL BLAS library based on this tutorial is now available at GitHub.
Note3: a WebGL2 demo of this tutorial is available at: https://www.ibiblio.org/e-notes/webgl/gpu/mul/sgemm.htm.
Background: Matrix-multiplication
Before we look at OpenCL code, let us define the computation we are about to perform. According to the definition of BLAS libraries, the single-precision general matrix-multiplication (SGEMM) computes the following:
C := alpha * A * B + beta * C
In this equation, A is a K by M input matrix, B is an N by K input matrix, C is the M by N output matrix, and alpha and beta are scalar constants. For simplicity, we assume the common case where alpha is equal to 1 and beta is equal to zero, yielding:
C := A * B
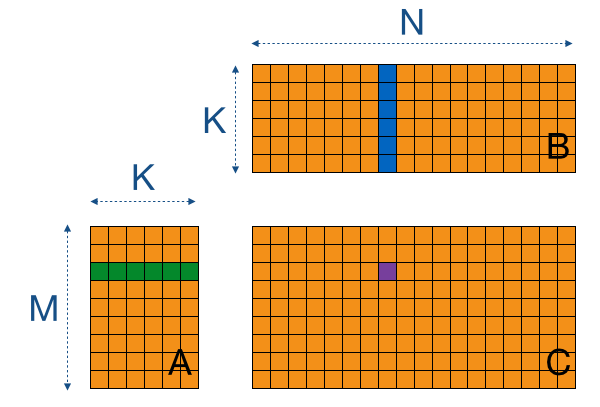
This computation is illustrated in the following image: to compute a single element of C (in purple), we need a row of A (in green) and a column of B (in blue).
This version of SGEMM can be implemented in plain C using 3 nested loops (see below). We assume data to be stored in column-major format (Fortran-style), following cuBLAS's default. If we wanted, we could easily change this to row-major by swapping the A and B matrices and the N and M constants, so this is not a real limitation of our code.
for (int m=0; m<M; m++) {
for (int n=0; n<N; n++) {
float acc = 0.0f;
for (int k=0; k<K; k++) {
acc += A[k*M + m] * B[n*K + k];
}
C[n*M + m] = acc;
}
}
To keep things simple for now, we assume that the matrix sizes are nice multiples of 32, such that we can for example create OpenCL workgroups of size 32 by 32 without having to worry about boundary conditions. There will be assumptions along these lines in the next couple of pages, but that's mainly because we want to keep the code simple and the main story-line easy to follow.
