Kernel 11: Evaluation of the clBlas SGEMM kernel

We have shown that we can do a lot better than clBlas. So, must we conclude that the developers of clBlas are not aware of any advanced techniques? That's probably not the right conclusion. Since clBlas was originally created by AMD, it might well be that their code is simply not optimised for the NVIDIA Tesla GPU that we tested on.

Let's first take a look at the un-tuned OpenCL code that clBlas uses. In the code below, there are a couple of things to notice:

1. The work-group size is fixed to 8x8.
2. Local memory is not used, meaning that there is no sharing of data within a work-group. On the plus size, this means that you don't have to care about synchronisation or local-memory bandwidth.
3. Both the input and output matrices are in vector format, i.e. data is loaded/stored as vectors.
4. Since local memory is not used and the matrix B is not transposed, we won't get coalesced accesses. This is partially solved however by the vector data-types.
5. By using vector data-types of 8-wide for A and 4-wide for B, clBlas implements a 8 by 4 2D register tiling. This implies that the inner computation loop can perform 4 times 4 times 8 or 128 FMAs before 4 new vector data-elements have to be loaded from off-chip memory.

typedef union GPtr {
    __global float *f;
    __global float2 *f2v;
    __global float4 *f4v;
    __global float8 *f8v;
    __global float16 *f16v;
} GPtr;

__attribute__((reqd_work_group_size(8, 8, 1)))
void __kernel
sgemmBlock(
    uint M,
    uint N,
    uint K,
    const float alpha,
    const float beta,
    const __global float8 *restrict A,
    const __global float4 *restrict B,
    __global float8 *C,
    uint lda,
    uint ldb,
    uint ldc)
{
    float8 a0, a1, a2, a3;
    float4 b0, b1, b2, b3;
    float8 c0, c1, c2, c3;
    uint4 coord = 0u; /* contains coordB, coordA, k */

    lda /= 8;
    ldb /= 4;
    A += (uint)get_global_id(0);
    B += 4u * (uint)get_global_id(1) * ldb;

    coord.y = 8u * (uint)get_global_id(0);
    coord.x = 4u * (uint)get_global_id(1);
    c0 = 0;
    c1 = 0;
    c2 = 0;
    c3 = 0;

    for (uint k1 = 0; k1 < K; k1 += 4) {
        /* -- Tiles multiplier -- */
        b0 = B[0];
        b1 = B[ldb];
        b2 = B[(ldb << 1)];
        b3 = B[mad24(3u, ldb, 0u)];

        a0 = A[0];
        a1 = A[lda];
        a2 = A[(lda << 1)];
        a3 = A[mad24(3u, lda, 0u)];

        c0 += a0 * b0.s0;
        c1 += a0 * b1.s0;
        c2 += a0 * b2.s0;
        c3 += a0 * b3.s0;

        c0 += a1 * b0.s1;
        c1 += a1 * b1.s1;
        c2 += a1 * b2.s1;
        c3 += a1 * b3.s1;

        c0 += a2 * b0.s2;
        c1 += a2 * b1.s2;
        c2 += a2 * b2.s2;
        c3 += a2 * b3.s2;

        c0 += a3 * b0.s3;
        c1 += a3 * b1.s3;
        c2 += a3 * b2.s3;
        c3 += a3 * b3.s3;

        A += (lda << 2);
        B += 1;
        /* ---------------------- */
    }


    GPtr uC;

    uC.f = C + (coord.x * ldc + coord.y)/8;

    __global float8 *pC = uC.f8v;

    float8 tempC0, tempC1, tempC2, tempC3;

    tempC0 = c0 * alpha + 0;
    tempC1 = c1 * alpha + 0;
    tempC2 = c2 * alpha + 0;
    tempC3 = c3 * alpha + 0;
    pC[0] = tempC0;
    pC[(ldc >> 3)] = tempC1;
    pC[(ldc >> 2)] = tempC2;
    pC[mad24(3u, (ldc >> 3), 0u)] = tempC3;
}

When we re-roll all unrolled loops and clean the code a bit (and re-write it in our own style), we obtain the myGEMM11 kernel. This kernel is essentially the same as the one above, and therefore also achieves the same performance.

// Settings
#define RX 8
#define RY 4
#define RK (RY)

// Mimic clBlas (4x8 register tiling with vector data-types)
__kernel void myGEMM11(const int M, const int N, const int K,
                       const __global float8* restrict A,
                       const __global float4* restrict B,
                       __global float8* C) {
    
    // Allocate register space
    float aReg[RK][RX];
    float bReg[RY][RK];
    float acc[RY][RX];

    // Initialise the accumulation registers
    for (int y=0; y<RY; y++) {
        for (int x=0; x<RX; x++) {
            acc[y][x] = 0.0;
        }
    }

    // Loop over all tiles
    const int numTiles = K/RK;
    for (int t=0; t<numTiles; t++) {

        // Load a tile of A and B into register memory
        for (int y=0; y<RY; y++) {

            // Load the data
            float8 aVec = A[(RK*t + y)*(M/RX) + get_global_id(0)];
            float4 bVec = B[(RY*get_global_id(1) + y)*numTiles + t];

            // Store the vector of A into registers
            aReg[y][0] = aVec.s0;
            aReg[y][1] = aVec.s1;
            aReg[y][2] = aVec.s2;
            aReg[y][3] = aVec.s3;
            aReg[y][4] = aVec.s4;
            aReg[y][5] = aVec.s5;
            aReg[y][6] = aVec.s6;
            aReg[y][7] = aVec.s7;

            // Store the vector of B into registers
            bReg[y][0] = bVec.x;
            bReg[y][1] = bVec.y;
            bReg[y][2] = bVec.z;
            bReg[y][3] = bVec.w;
        }

        // Perform the computations
        for (int k=0; k<RK; k++) {
            for (int y=0; y<RY; y++) {
                for (int x=0; x<RX; x++) {
                    acc[y][x] += aReg[k][x] * bReg[y][k];
                }
            }
        }
    }

    // Store the final results in C
    for (int y=0; y<RY; y++) {
        float8 accVec;
        accVec.s0 = acc[y][0];
        accVec.s1 = acc[y][1];
        accVec.s2 = acc[y][2];
        accVec.s3 = acc[y][3];
        accVec.s4 = acc[y][4];
        accVec.s5 = acc[y][5];
        accVec.s6 = acc[y][6];
        accVec.s7 = acc[y][7];
        C[(y + RY*get_global_id(1))*(M/RX) + get_global_id(0)] = accVec;
    }
}

Since our own version contains loops and uses defines for the register-tiling size, we can actually experiment with other tiling options (note that we do have to support other vector-data types, see the GitHub repository for the full version of myGEMM11). The performance numbers below show that simply tuning one of the parameters of clBlas allows us to squeeze out a bit more performance.

On a side note, the CUDA version of the same OpenCL doesn't perform so well (~300 GFLOPS). Only after we move to a 4 by 4 register-tiling configuration can the CUDA back-end reduce register pressure enough to perform better than its OpenCL counter-part.



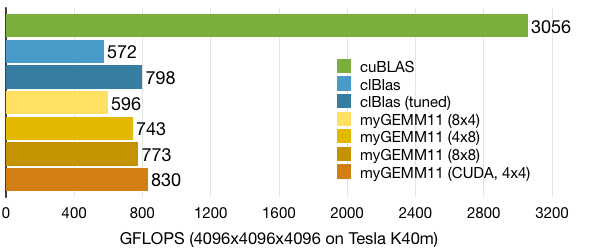
Additionally, clBlas provides an auto-tuning script, which delivers slightly better performance on NVIDIA hardware. We haven't investigated the auto-tuned version nor the auto-tuning script in details.

cnugteren.github.io