Kernel 5: Transposed input matrix and rectangular tiles

Our first tiled version showed that a large tile size can greatly reduce off-chip memory accesses and can thus improve performance. However, if we want to go to even larger tiles (say 64 by 64) we'll run out of resources. The Tesla K40 GPU which we use has 48KB of local memory per SM, on which multiple work-groups can run. For a 32 by 32 tile, this means we consume 2*32*32*4 = 8KB per work-group, so there is some headroom left.

To get more flexibility and to be able to fine-tune the parameters, we'll want to go for rectangular tiles. Since both matrix A and B share the dimension K, we can actually create rectangular tiles, as is shown in the image below. In the example picture, we'll have to iterate over 3 tiles of 3x2 each, while we are still computing a 3x3 tile in the end.



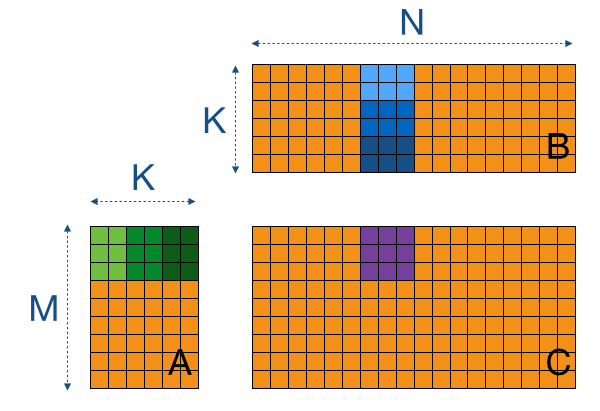
To get this idea implemented, we'll want to transpose one of the input matrices before starting the matrix-multiplication. This will save us a lot of trouble computing indices, as the K-sized dimension (which A and B share) will be the same dimension. We choose to transpose the B matrix.

The transpose kernel itself is actually quite trivial and is negligible in terms of computational cost compared to the main matrix-multiplication kernel. Here is the transpose kernel which we used:

// Simple transpose kernel for a P * Q matrix
__kernel void transpose(const int P, const int Q,
                        const __global float* input,
                        __global float* output) {
    
    // Thread identifiers
    const int tx = get_local_id(0);
    const int ty = get_local_id(1);
    const int ID0 = get_group_id(0)*TRANSPOSEX + tx; // 0..P
    const int ID1 = get_group_id(1)*TRANSPOSEY + ty; // 0..Q

    // Set-up the local memory for shuffling
    __local float buffer[TRANSPOSEX][TRANSPOSEY];

    // Swap the x and y coordinates to perform the rotation (coalesced)
    if (ID0 < P && ID1 < Q) {
        buffer[ty][tx] = input[ID1*P + ID0];
    }

    // Synchronise all threads
    barrier(CLK_LOCAL_MEM_FENCE);

    // We don't have to swap the x and y thread indices here,
    // because that's already done in the local memory
    const int newID0 = get_group_id(1)*TRANSPOSEY + tx;
    const int newID1 = get_group_id(0)*TRANSPOSEX + ty;

    // Store the transposed result (coalesced)
    if (newID0 < Q && newID1 < P) {
        output[newID1*Q + newID0] = buffer[tx][ty];
    }
}

Now, let's see what the new matrix-multiplication kernel looks like. We'll take our earlier kernel with an increased work per thread count (WPT) as a starting point. First, let us define some new constants:

#define TSM 64                 // The tile-size in dimension M
#define TSN 64                 // The tile-size in dimension N
#define TSK 32                 // The tile-size in dimension K
#define WPTN 8                 // The work-per-thread in dimension N
#define RTSN (TSN/WPTN)        // The reduced tile-size in dimension N
#define LPT ((TSK*TSM)/(RTSM*RTSN)) // The loads-per-thread for a tile

Note that, although we do define separate tile-sizes in the M and N dimensions, we assume for now they are equal. As before, we use the WPT setting to reduce the amount of threads in the second thread dimension. Our launch-parameters are:

const size_t local[2] = { TSM, TSN/WPTN }; // Or { TSM, RTSN };
const size_t global[2] = { M, N/WPTN };

Our kernel looks a lot like our 3rd version. The most notable differences are:

• Since matrix B is transposed, reading the inputs A and B is now very similar. The main difference between the two is that outside of a work-group, work-group IDs determine which tile to load.
• Because matrix B is transposed, we'll have to un-transpose data in the local memory. There are two options:
  1. We could access the Bsub matrix in the inner computational loop as [k,col] instead of [col,k]. However, that would mean that subsequent iterations of the k-loop no longer require subsequent data from the local memory. Is this bad? Actually, yes, since the compiler can replace 2 32-bit loads from the local memory (LDS) with one 64-bit load (LDS.64) as long as data is well positioned and aligned. These 64-bit (or 128-bit) loads not only save instructions, but are also the only way to benefit from the full bandwidth of the GPU's local memory (and we might actually saturate the bandwidth!).
  2. Since we don't want to change the access pattern to the local memory (see point 1), we'll have to change the way data is stored into the local memory (otherwise results will simply be incorrect). This can be done by changing the original [col,row] pattern (as still is used for matrix A) into a [row,col] storing pattern (see the new code below). This has a new drawback: bank conflicts. We'll discuss that later.
• The constant TS has been replaced with either TSK, TSM, or TSN. Special care has to be taken with respect to the amount of loads per tile, as this is no longer equal to the WPT setting. In fact, the tile-size changes with TSK, whereas the number of threads in a work-group changes with TSM and TSN. Note that the code poses some constraints on the settings, for example LPT has to be an integer. If not, code will grow complicated very quickly and performance will drop due to branches.

// Pre-transpose the input matrix B and use rectangular tiles
__kernel void myGEMM5(const int M, const int N, const int K,
                      const __global float* A,
                      const __global float* B,
                      __global float* C) {
    
    // Thread identifiers
    const int row = get_local_id(0); // Local row ID (max: TSM)
    const int col = get_local_id(1); // Local col ID (max: TSN/WPTN)
    const int globalRow = TSM*get_group_id(0) + row; // 0..M
    const int globalCol = TSN*get_group_id(1) + col; // 0..N

    // Local memory to fit a tile of A and B
    __local float Asub[TSK][TSM];
    __local float Bsub[TSN][TSK];

    // Initialise the accumulation registers
    float acc[WPTN];
    for (int w=0; w<WPTN; w++) {
        acc[w] = 0.0f;
    }
    
    // Loop over all tiles
    int numTiles = K/TSK;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        for (int l=0; l<LPT; l++) {
            int tiledIndex = TSK*t + col + l*RTSN;
            int indexA = tiledIndex*M + TSM*get_group_id(0) + row;
            int indexB = tiledIndex*N + TSN*get_group_id(1) + row;
            Asub[col + l*RTSN][row] = A[indexA];
            Bsub[row][col + l*RTSN] = B[indexB];
       }
        
        // Synchronise to make sure the tile is loaded
        barrier(CLK_LOCAL_MEM_FENCE);

        // Perform the computation for a single tile
        for (int k=0; k<TSK; k++) {
            for (int w=0; w<WPTN; w++) {
                acc[w] += Asub[k][row] * Bsub[col + w*RTSN][k];
            }
        }

        // Synchronise before loading the next tile
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // Store the final results in C
    for (int w=0; w<WPTN; w++) {
        C[(globalCol + w*RTSN)*M + globalRow] = acc[w];
    }
}

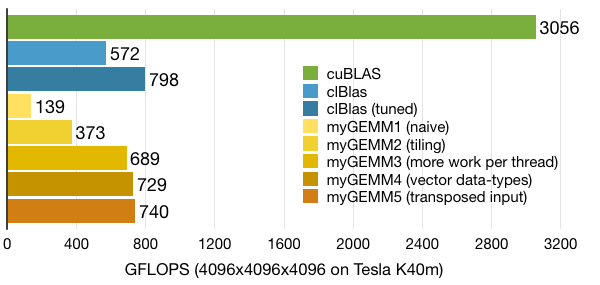
Using the same settings as before (squared tiles of 32 by 32 and a WPT of 8) we achieve only 460 GFLOPS, less than the 689 of the earlier kernel. The decreased performance is caused by bank-conflicts in the local memory in the following line:

Bsub[row][col + w*RTSN] = B[indexB];

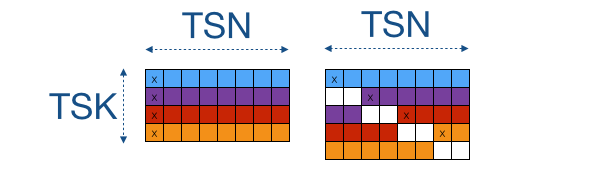
The bank-conflicts arise because threads within a warp (same 'col' value, but different 'row' value) access the same (or many of the same) local memory banks. The image below on the left visualises this: threads in a warp (4 for this toy-example) access data in a column-wise fashion. For example, the first warp will access all elements marked with an 'x'. On our Kepler GPU, local memory is arranged in 32 banks. If TSN is equal to 32, then every column in the picture represents a single bank (let's not consider the different addressing modes for simplicity). To repair this we have to make sure that threads in a warp do not access the same column. A well-known technique is to use padding:

__local float Bsub[TSN][TSK+2];

Padding by 2 will result in the picture on the right, in which we can see that bank conflicts no longer occur (or at least a lot less than before). Note that we pad the memory by 2 rather than 1 to align data to 64-bit (two floats) so that we can still benefit from 64-bit loads from local memory. You probably noted that the padding does consume extra local memory, so this technique might deteriorate performance if occupancy is reduced and latency can no longer be hidden.



Now that we have all of this working, we have the freedom to select 64 by 32 blocks for example. This gives us a little bit of extra performance over the earlier kernel's 32 by 32 blocks, giving us 740 GFLOPS.

cnugteren.github.io