Kernel 4: Wider data-types

In the previous kernel we increased the amount of work in the column-dimension of C. Obviously, we could have also done this in the row-dimension (or in both, but we'll explore this later). Although this has the same advantage of reducing pressure on the local memory, it can have another advantage: wider data-types. Why is this? Well, increasing the work per thread in the row-dimension of C can also be done by considering vector data-types instead of loops over WPT. The NVIDIA GPUs don't support vector operations (such as multiply or add) in hardware, but they do have special wider load and store instructions both for the off-chip and the local memory. Let's see if using them gives us better performance.

First, we set the launch-parameters of our new kernel considering that we'll use data-types of width 'WIDTH':

const size_t local[2] = { TS/WIDTH, TS };
const size_t global[2] = { M/WIDTH, N };

OpenCL already defines floating-point vector types, which makes using them quite convenient. And we also don't have to transform our matrices into vector types: we can simply cast the pointers in our kernel. To remain flexible, we'll create a new data-type to be able to configure the WIDTH parameter with a pre-processor define:

#define WIDTH 4
#if WIDTH == 1
    typedef float floatX;
#elif WIDTH == 2
    typedef float2 floatX;
#elif WIDTH == 4
    typedef float4 floatX;
#endif

The new kernel is given below. We have left out support for the float8 data-type to make the code more readable, although WIDTH is actually set to 8 for our benchmark, as this gives the best performance. The kernel is based on the same concept that we used for the previous kernel, but there are a few changes: The increased amount of work per thread is now found in dimension 0 (rows of C) rather than 1 (columns of C). Since the data-types are now vectors, all indices have to be divided by a factor WIDTH. The inner-loop computation has to be written out, as it is not a vector FMA operation. An alternative solution is to use a scalar pointer to local memory and a regular loop.

// Use wider data types
__kernel void myGEMM4(const int M, const int N, const int K,
                      const __global floatX* A,
                      const __global floatX* B,
                      __global floatX* C) {
    
    // Thread identifiers
    const int row = get_local_id(0); // Local row ID (max: TS/WIDTH)
    const int col = get_local_id(1); // Local col ID (max: TS)
    const int globalRow = (TS/WIDTH)*get_group_id(0) + row; // 0..M/WIDTH
    const int globalCol = TS*get_group_id(1) + col; // 0..N

    // Local memory to fit a tile of TS*TS elements of A and B
    __local floatX Asub[TS][TS/WIDTH];
    __local floatX Bsub[TS][TS/WIDTH];

    // Initialise the accumulation registers
    #if WIDTH == 1
        floatX acc = 0.0f;
    #elif WIDTH == 2
        floatX acc = { 0.0f, 0.0f };
    #elif WIDTH == 4
        floatX acc = { 0.0f, 0.0f, 0.0f, 0.0f };
    #endif
    
    // Loop over all tiles
    const int numTiles = K/TS;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        const int tiledRow = (TS/WIDTH)*t + row;
        const int tiledCol = TS*t + col;
        Asub[col][row] = A[tiledCol*(M/WIDTH) + globalRow];
        Bsub[col][row] = B[globalCol*(K/WIDTH) + tiledRow];
       
        // Synchronise to make sure the tile is loaded
        barrier(CLK_LOCAL_MEM_FENCE);

        // Perform the computation for a single tile
        floatX vecA, vecB;
        float valB;
        for (int k=0; k<TS/WIDTH; k++) {
            vecB = Bsub[col][k];
            for (int w=0; w<WIDTH; w++) {
                vecA = Asub[WIDTH*k + w][row];
                #if WIDTH == 1
                    valB = vecB;
                    acc += vecA * valB;
                #elif WIDTH == 2
                    switch (w) {
                        case 0: valB = vecB.x; break;
                        case 1: valB = vecB.y; break;
                    }
                    acc.x += vecA.x * valB;
                    acc.y += vecA.y * valB;
                #elif WIDTH == 4
                    switch (w) {
                        case 0: valB = vecB.x; break;
                        case 1: valB = vecB.y; break;
                        case 2: valB = vecB.z; break;
                        case 3: valB = vecB.w; break;
                    }
                    acc.x += vecA.x * valB;
                    acc.y += vecA.y * valB;
                    acc.z += vecA.z * valB;
                    acc.w += vecA.w * valB;
               #endif
            }
        }

        // Synchronise before loading the next tile
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // Store the final results in C
    C[globalCol*(M/WIDTH) + globalRow] = acc;
}

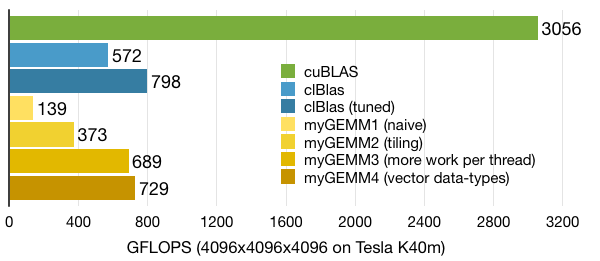
This kernel performs a bit better than the previous kernel due to its wider data-types and thus fewer load/store instructions. But the real benefit will be apparent later on when we will combine these two techniques.

cnugteren.github.io