Kernel 2: Tiling in the local memory

The main reason the naive implementation doesn't perform so well is because we are accessing the GPU's off-chip memory way too much. Please count with me: to do the M*N*K multiplications and additions, we need M*N*K*2 loads and M*N stores. Since the multiplications and additions can actually be fused into a single hardware instruction (FMA), the computational intensity of the code is only 0.5 instructions per memory access (search for the "Roofline model" to find out why this is bad). Although the GPU's caches probably will help us out a bit, we can get much more performance by manually caching sub-blocks of the matrices (tiles) in the GPU's on-chip local memory (== shared memory in CUDA).

To compute a sub-block Csub of C (purple tile in the image below), we need A's corresponding rows (in green) and B's corresponding columns (in blue). Now, if we also divide A and B in sub-blocks Asub and Bsub, we can iteratively update the values in Csub by summing up the results of multiplications of Asub times Bsub.



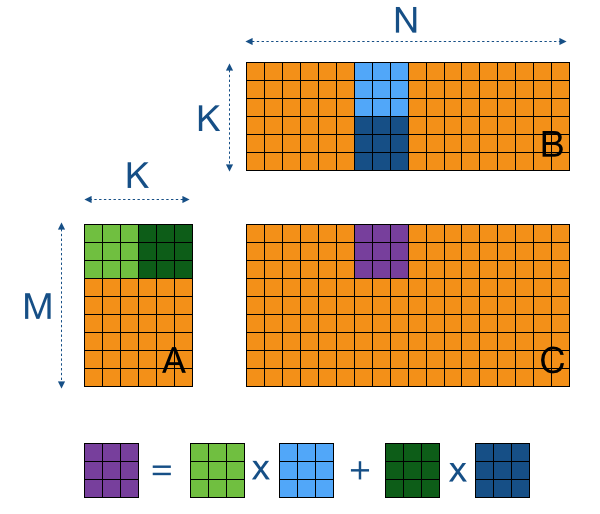
Why is this useful? Well, if we take a closer look at the computation of a single element (in the image below), we see that there is lots of data re-use within a tile. For example, in the 3x3 tiles of the image below, all elements on the same row of the purple tile (Csub) are computed using the same data of the green tiles (Asub).



Let's translate this abstract image into actual OpenCL code. The trick here is to share the data of the Asub and Bsub tiles within a work-group (== threadblock in CUDA) via the local memory. To maximise the benefit of re-use, we'll make these tiles as large as possible.

To implement tiling, we'll leave our host code from the previous naive kernel intact. Note that it uses 2D work-groups of 32 by 32 (or TS x TS). This means that the purple Csub tile is also 32 by 32. For now, let's also take these dimensions for the Asub and Bsub tiles, we'll investigate rectangular tiles later on.

// Tiled and coalesced version
__kernel void myGEMM2(const int M, const int N, const int K,
                      const __global float* A,
                      const __global float* B,
                      __global float* C) {
    
    // Thread identifiers
    const int row = get_local_id(0); // Local row ID (max: TS)
    const int col = get_local_id(1); // Local col ID (max: TS)
    const int globalRow = TS*get_group_id(0) + row; // Row ID of C (0..M)
    const int globalCol = TS*get_group_id(1) + col; // Col ID of C (0..N)

    // Local memory to fit a tile of TS*TS elements of A and B
    __local float Asub[TS][TS];
    __local float Bsub[TS][TS];

    // Initialise the accumulation register
    float acc = 0.0f;
    
    // Loop over all tiles
    const int numTiles = K/TS;
    for (int t=0; t<numTiles; t++) {

        // Load one tile of A and B into local memory
        const int tiledRow = TS*t + row;
        const int tiledCol = TS*t + col;
        Asub[col][row] = A[tiledCol*M + globalRow];
        Bsub[col][row] = B[globalCol*K + tiledRow];

        // Synchronise to make sure the tile is loaded
        barrier(CLK_LOCAL_MEM_FENCE);

        // Perform the computation for a single tile
        for (int k=0; k<TS; k++) {
            acc += Asub[k][row] * Bsub[col][k];
        }

        // Synchronise before loading the next tile
        barrier(CLK_LOCAL_MEM_FENCE);
    }

    // Store the final result in C
    C[globalCol*M + globalRow] = acc;
}

If we take a look at the code, we see that the original accumulation loop over K has been split into two new loops: one over all K/TS tiles and one over all TS elements within a tile. Within this loop over the tiles, we can identify two parts which are separated with synchronisation barriers: (1) loading from off-chip memory to local memory, and (2) computation based on local memory data. Note that each thread now performs only two global loads per tile (one element of A and B), whereas this used to be two times the tile-size (a row of A and a column of B). This gives us a reduction of a factor 32 in off-chip memory accesses!

There is one other thing to notice: since we are now loading tiles instead of columns from B, and since we are now sharing them within a work-group, we can replace un-coalesced memory accesses by coalesced counter-parts by loading them per row.

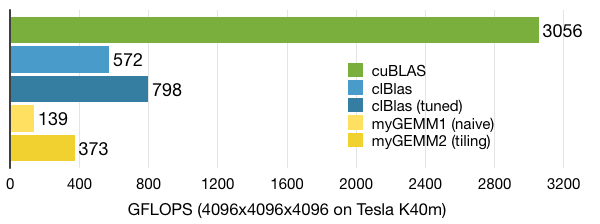
When we look at performance, we see a great improvement over the naive implementation. However, with ~370 GFLOPS we are still not at the level of clBLAS, so there is much more work to!

cnugteren.github.io